| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 회귀분석
- ADsP
- 태블로
- Deep Learning Specialization
- 자격증
- 이것이 코딩테스트다
- 머신러닝
- 통계
- 데이터분석
- pytorch
- pandas
- IRIS
- Python
- tableau
- 딥러닝
- r
- sklearn
- 파이썬
- SQL
- scikit learn
- matplotlib
- Google ML Bootcamp
- 데이터 분석
- 데이터 전처리
- SQLD
- 코딩테스트
- 시각화
- ML
- 이코테
- 데이터분석준전문가
- Today
- Total
함께하는 데이터 분석
규제 회귀 모델 본문
오늘은 규제 회귀 모델인
Lasso, Ridge, ElasticNet Regression에 대해 알아보겠습니다.
규제 회귀 모델 사용 배경
규제 회귀 모델 이전에 우리들이 많이들 알고 있는 선형 회귀 모형이 있습니다.
회귀모델의 목적은 크게 2가지입니다.
독립변수들의 연관성과 미래 데이터의 예측이죠.
그래서 예측력을 높이기 위해 학습 데이터에 지나치게 맞추게 되고
과적합(overfitting)의 문제가 발생하게 됩니다.
그래서 overfitting의 문제를 해결하기 위해
overfitting 된 파라미터에 페널티를 부여하는
규제 회귀모델이 등장합니다.
Lasso Regression
L1-norm 페널티항으로 회귀모델에 페널티를 부과하여 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수 크기를 0에 가깝게 작게 만들거나 0으로 만드는 모델

𝛼값이 0이면 선형 회귀모델
𝛼값이 커지면 최소가 되기 위해 회귀계수의 값이 작아져 과적합 방지 가능
특징
- 독립 변수를 선택하여 사용이 가능(회귀 계수를 0으로 만들 수 있음)
- 독립 변수 간의 상관관계가 높은 경우 Ridge에 비해 성능이 떨어짐
Ridge Regression
L2-norm 페널티항으로 회귀모델에 페널티를 부과하여 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수 크기를 0에 가깝게 작게 만드는 모델
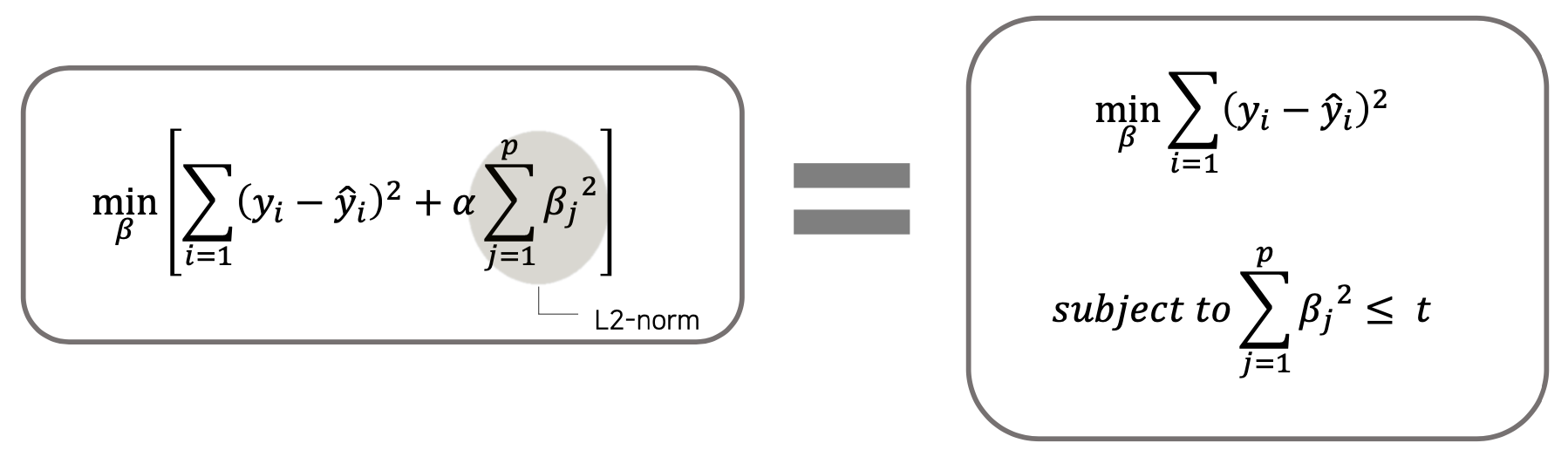
𝛼값이 0이면 선형 회귀모델
𝛼값이 커지면 최소가 되기 위해 회귀계수의 값이 작아져 과적합 방지 가능
특징
- 모든 독립변수를 사용해야 함(회귀 계수를 0으로 만들 수 없음)
- 독립 변수 간의 상관관계가 높은 경우도 좋은 예측력을 가짐
- 크기가 큰 변수를 우선적으로 줄이는 경향이 있음
ElasticNet Regression
L1-norm과 L2-norm 페널티항을 모두 이용하여 회귀모델에 페널티를 부과하는 모델
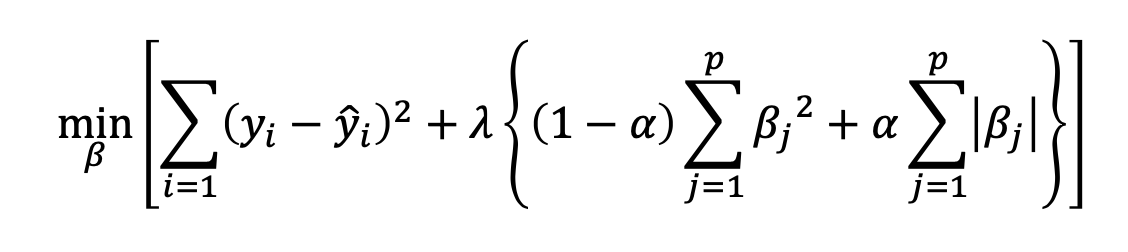
𝜆 : 페널티 튜닝 파라미터
𝛼 : 라쏘 회귀 모델과 릿지 회귀모델의 혼합 정도를 결정하는 파라미터
𝛼 = 1이면 라쏘 회귀모델, 𝛼 = 0이면 릿지 회귀모델
총정리
- 과적합된 모델을 단순화하여 일반화된 모델로 만듦
- 페널티를 준다는 것은 편향을 높인다는 것
- 페널티를 추가하면 규제가 없는 회귀 모델보다 계수의 절댓값이 작아져 overfitting 방지
- 독립변수의 척도에 영향을 많이 받으므로 규제를 사용하기 전 표준화를 해야 함
Copyright
- 비어플 빅데이터 학회
'학회 세션 > 비어플' 카테고리의 다른 글
| [Python] 규제 회귀 모델 (0) | 2022.04.02 |
|---|---|
| [R] 로지스틱 회귀 & LDA (0) | 2022.03.26 |
| [Classification] LDA(선형 판별분석) (0) | 2022.03.26 |
| [Python] IMAGE(2D data) AUGMENTATION (0) | 2022.03.24 |
| [R] 데이터 불균형 해소 (0) | 2022.03.20 |




