| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- ML
- tableau
- 코딩테스트
- 머신러닝
- 데이터 분석
- scikit learn
- 데이터분석준전문가
- 자격증
- 데이터분석
- Deep Learning Specialization
- 파이썬
- pandas
- sklearn
- ADsP
- r
- pytorch
- IRIS
- 회귀분석
- SQL
- 통계
- 딥러닝
- 데이터 전처리
- 이코테
- SQLD
- 이것이 코딩테스트다
- Google ML Bootcamp
- Python
- matplotlib
- 시각화
- 태블로
- Today
- Total
함께하는 데이터 분석
[회귀분석] Simple linear regression 검정 본문
오늘은 simple linear regression에서
검정(test)을 공부해보겠습니다.
귀무가설 대립가설 세우기

우리는 simple linear regression에서
β_0인 intercept 부분보다
β_1인 기울기 부분에 관심이 있습니다.
그래서 귀무가설에 β_1 = 0을 놓고
우리가 궁금해하는 대립가설에 β_1 =/ 0으로 설정했습니다.
일반적인 가설검정이라고 볼 수 있죠.
그런데 저번 포스트에서 M_0 모델과 M_1 모델을 살펴본 것이 기억나세요?
모델의 관점에서 M_0 모델이 옳은가, M_1 모델이 옳은가로 가설검정을 세우면
위의 기울기의 관점과 동치가 됩니다.
M_0 모델은 x_i인 설명변수가 없는 모델이지만
M_1 모델에서 β_1이 0이 되면 x_i가 의미가 없어지기 때문이죠.
그렇다면 가설검정이 동치이니
T(test statistics)도 비슷해야 할 것입니다.
이제 test statistics를 알아보겠습니다.
기울기 관점에서의 test statistics

β_1의 추정값은 unbiased estimator이므로
위와 같이 정규분포를 따릅니다.
표준화를 시킬 수 있죠.
하지만 표준 정규분포를 test statistics로 사용하기에는 무리가 있습니다.
우리가 모르는 모수인 σ가 있기 때문이죠.
그렇다면 σ를 표본 표준편차로 바꿔볼까요?
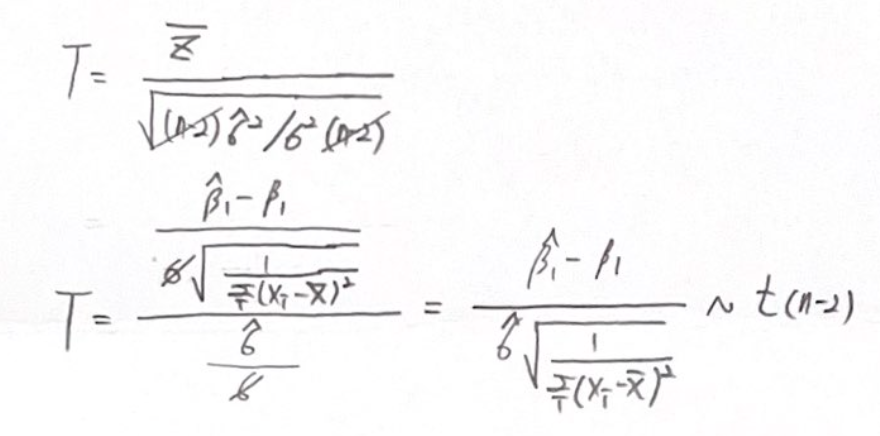
독립인 표준 정규분포와 카이제곱 분포를 이용하여
자유도가 n-2인 t분포로 만들어줬습니다.
이번에는 모델 관점에서의 test statistics를 알아보겠습니다.
모델 관점에서의 test statistics
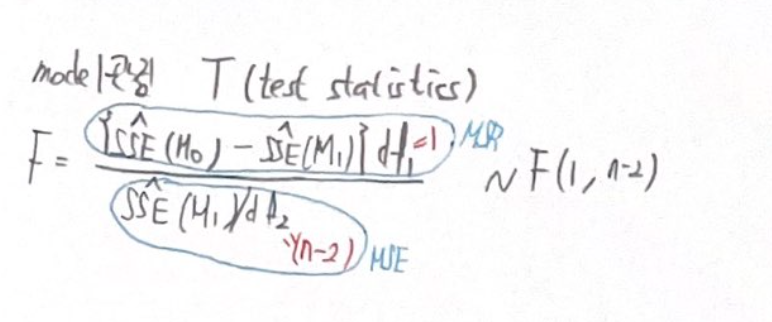
model 관점에서의 test statistics는
자유도가 (1, n-2)인 F분포를 따릅니다.
그렇다면 모델 관점의 가설검정과
기울기 관점의 가설검정이 동치인데
test statistics는 어떤 관계가 있을까요?

기울기 관점에서의 test statistics의 제곱이
모델 관점에서의 test statistics와 일치합니다.
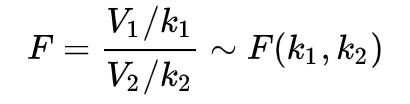
(카이제곱 분포 1/자유도 1)/(카이제곱 분포 2/자유도 2)는
정의에 따라 자유도가 (자유도 1, 자유도 2)인
F분포를 따르기 때문이죠.
지금까지 simple linear regression의 검정부분까지 살펴봤으니
다음은 R을 이용하여 지금까지의 이론을 바탕으로
구현해보는 시간을 갖겠습니다.
'통계학과 수업 기록 > 회귀분석' 카테고리의 다른 글
| [회귀분석] Simple Linear Regression with R (0) | 2022.04.14 |
|---|---|
| [회귀분석] SSE와 결정계수 R^2 (0) | 2022.04.03 |
| [회귀분석] Simple linear regression LSE·MLE (0) | 2022.03.26 |
| [회귀분석] 선형회귀분석 개요② (0) | 2022.03.12 |
| [회귀분석] 선형회귀분석 개요① (0) | 2022.03.08 |




