| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Google ML Bootcamp
- 데이터분석
- 회귀분석
- 코딩테스트
- 태블로
- 시각화
- 머신러닝
- Python
- SQL
- tableau
- sklearn
- ADsP
- 데이터분석준전문가
- SQLD
- 이코테
- 통계
- IRIS
- 파이썬
- matplotlib
- pandas
- r
- pytorch
- 데이터 분석
- 딥러닝
- ML
- Deep Learning Specialization
- 자격증
- 이것이 코딩테스트다
- 데이터 전처리
- scikit learn
- Today
- Total
목록회귀분석 (6)
함께하는 데이터 분석
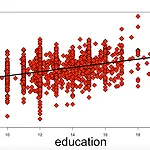 [회귀분석] Simple Linear Regression with R
[회귀분석] Simple Linear Regression with R
오늘은 R을 이용하여 simple linear regression을 알아보겠습니다. 데이터는 wages.Rdata를 사용했습니다. 데이터 불러오기 setwd("경로") load("wages.Rdata") attach(wages) setwd를 통하여 자신의 경로를 설정한 다음 load를 통해 경로 안에 있는 파일을 불러오면 됩니다. attach를 통하여 데이터를 불러옴으로써 data.frame에서 column을 wages$logwage가 아닌 logwage라고 쓸 수 있게 됩니다. 데이터 구조 파악하기 str(wages) >>> 'data.frame':2178 obs. of 2 variables: $ education: num 16.8 15 10 12.7 15 ... $ logwage : num 2.85 ..
 [회귀분석] Simple linear regression 검정
[회귀분석] Simple linear regression 검정
오늘은 simple linear regression에서 검정(test)을 공부해보겠습니다. 귀무가설 대립가설 세우기 우리는 simple linear regression에서 β_0인 intercept 부분보다 β_1인 기울기 부분에 관심이 있습니다. 그래서 귀무가설에 β_1 = 0을 놓고 우리가 궁금해하는 대립가설에 β_1 =/ 0으로 설정했습니다. 일반적인 가설검정이라고 볼 수 있죠. 그런데 저번 포스트에서 M_0 모델과 M_1 모델을 살펴본 것이 기억나세요? 모델의 관점에서 M_0 모델이 옳은가, M_1 모델이 옳은가로 가설검정을 세우면 위의 기울기의 관점과 동치가 됩니다. M_0 모델은 x_i인 설명변수가 없는 모델이지만 M_1 모델에서 β_1이 0이 되면 x_i가 의미가 없어지기 때문이죠. 그렇다면..
 [회귀분석] SSE와 결정계수 R^2
[회귀분석] SSE와 결정계수 R^2
오늘은 SSE와 결정계수(R^2)에 대해 알아보겠습니다. 저번 시간에 SSE에 대해서 알아봤는데 오늘은 2가지 model에 대해 SSE를 알아보겠습니다. M_0 model의 SSE m_0 model은 독립변수인 x_i가 없는 모델입니다. 빨간색 x표시가 observation인데 Y축 위에 있는 것을 볼 수 있죠. 이때 SSE는 위와 같습니다. SSE는 Sum of Square Estimation의 약자이죠. M_1 model의 SSE M_1 model이 우리가 알고 있는 simple linear regression입니다. M_1의 SSE가 우리가 말하는 일반적인 SSE입니다. M_0과 M_1 model의 SSE비교 observarion에서 회귀선으로 내린 선분의 제곱한 값이 SSE인 것은 다들 알고 계실..
 [회귀분석] 선형회귀분석 개요②
[회귀분석] 선형회귀분석 개요②
오늘은 이어서 회귀분석 때 사용할 가설검정 과정, CLT, CI에 대해 알아보겠습니다. 위의 식에서 모수 B1의 값을 구했을 때 제대로 구했는지 가설검정을 해야 합니다. 귀무가설을 베타1 = 0 대립 가설을 베타1 =/ 0이라고 놓습니다. 만약 베타1이 0이면 엄마의 키 변수가 딸의 키에 영향을 미치지 않으므로 위의 회귀식은 의미가 없어지게 되니까요. 그렇다면 가설검정의 단계를 알아볼까요? 첫 번째로 귀무가설과 대립가설을 설정하고 두 번째로 유의수준 알파를 정합니다. 이후에 분포를 찾고 p-value값을 계산합니다. 마지막으로 p-value값과 알파 값을 비교하여 p-value값이 알파 값보다 작다면 귀무가설을 기각하고 크다면 귀무가설을 기각하지 못합니다. 여기서 중요한 것은 귀무가설을 채택한다고 표현하..
 [R] 선형회귀를 이용한 회귀분석
[R] 선형회귀를 이용한 회귀분석
안녕하세요! 오늘은 선형회귀를 이용한 의료비 예측하는 간단한 예제를 살펴볼게요. 위 파일을 사용할 것입니다. 변수명 변수설명 Age 주 수익자의 연령, 정수(64세 이상은 일반적으로 정부에서 관리하기 때문에 제외) Sex 보험 계약자의 성별, 여성 또는 남성 Bmi 몸무게(kg)을 키(m)의 제곱으로 나눈 값 Children 의료보험이 적용되는 자녀 수/부양가족 수. 정수 Smoker 피보험자의 정기적인 흡연 여부, 예 또는 아니오, 범주형 변수 Region 사는 지역, 범주형 변수 Expenses 종속변수 위의 표가 변수에 관한 설명입니다. 이제 시작해볼까요? 1. 데이터 불러오기 setwd("경로") insurance >> [1] 1338 7 head(insurance) >>> age sex bmi ..
 [회귀분석] 선형회귀분석 개요①
[회귀분석] 선형회귀분석 개요①
안녕하세요! 오늘은 회귀분석을 본격적으로 배우기 전 필요한 기본지식과 대략적인 소개를 하는 시간입니다. 제가 공부할 회귀분석 모델은 선형회귀분석(linear regression model)입니다. 독립변수 여러개와 종속변수 1개인 모델입니다. 종속변수가 범주형인 0과 1로 나옴에 따라 로지스틱회귀분석(logistic regression model) 이라는 것도 있지만 여기서는 다루지 않습니다. 다음학기에 범주형 자료 분석 때 기회가 된다면 살펴볼 예정입니다! 그리고 우리는 average outcome을 기반으로 할 것입니다. 평균이 아닌 중위수를 기반으로 하는 quantile regression도 있지만 여기서는 다루지 않습니다ㅠㅠ 그럼 본격적으로 시작해볼까요? 회귀분석에서 중요한 관점은 2가지 Asso..
