| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 코딩테스트
- r
- scikit learn
- 머신러닝
- SQLD
- 데이터분석준전문가
- ML
- 태블로
- Google ML Bootcamp
- Python
- tableau
- pandas
- matplotlib
- 자격증
- 딥러닝
- sklearn
- 데이터분석
- 파이썬
- 회귀분석
- 이것이 코딩테스트다
- SQL
- pytorch
- IRIS
- 시각화
- Deep Learning Specialization
- 데이터 전처리
- 통계
- 이코테
- ADsP
- 데이터 분석
- Today
- Total
함께하는 데이터 분석
[Find-A] [Scikit Learn] 로지스틱 회귀 본문
안녕하세요!
오늘은 로지스틱 회귀모형을 Python으로 돌려보겠습니다.
다른 포스팅에도 개념은 설명되어 있어 간단하게 말하고 넘어갈게요.
로지스틱 회귀는 이진 분류기로 샘플이 특정 클래스에 속할 확률을 추정합니다.
추정 확률이 50%가 넘으면 그 샘플이 해당 클래스에 속한다고 예측합니다.
0 이면 음성 클래스, 1이면 양성 클래스로 보통 분류합니다.
이제 Python의 iris데이터를 활용하여 분류해볼게요!
라이브러리 불러오기
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import sklearn
import warnings
warnings.filterwarnings('ignore')사실 이번 로지스틱 회귀로 분류할 때 필요 없는 라이브러리도 있지만
데이터 분석을 할 때 자주 쓰는 라이브러리로
저는 고정으로 복붙 형식으로 불러오는 편입니다.
이제 사이킷런으로 iris 데이터를 불러올게요.
데이터 불러오기
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
iris
이렇게 iris 데이터가 array 형식으로 되어있습니다.
좀 이따 제대로 분류했는지 확인할 때 데이터 프레임으로 바꿔서
진행해볼게요!
X = iris['data'][:, 3:] # 꽃잎의 너비
y = (iris['target'] == 2).astype(np.int) # Virginica면 1, 아니면 0X에 iris 데이터의 모든 행 4번째 열인 꽃잎의 너비를 할당하고
y에 iris의 Virginica를 할당했습니다.
로지스틱 회귀 모형
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X, y)
로지스틱 회귀모형을 꽃잎의 너비를 기반으로 Virginica 종을 감지하는
분류기를 만들었습니다.
이제 꽃잎의 너비가 0~3인 꽃에 대해 모델의 추정 확률을 계산해볼게요.
X_new = np.linspace(0, 3, 1000).reshape(-1, 1) # 0~3 사이 1000개
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], 'g-', label='Iris-Virginica')
plt.plot(X_new, y_proba[:, 0], 'b--', label='Iris-Virginica 아님')
plt.show()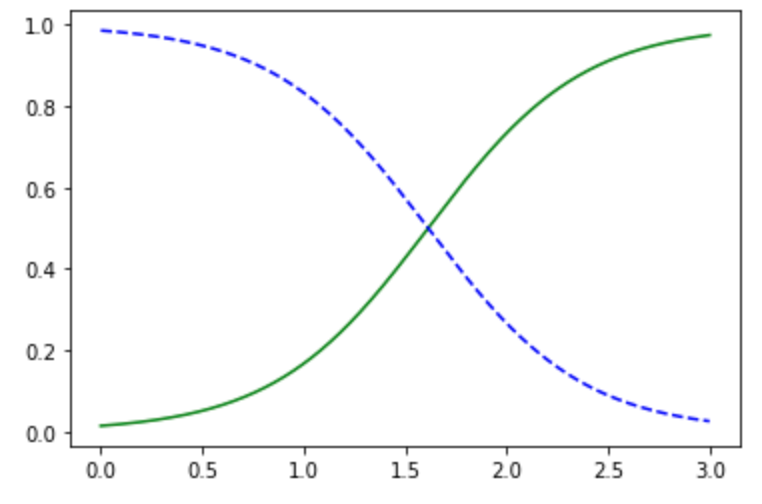
꽃잎의 너비가 1.6 정도에서 결정 경계가 형성되는 것을 볼 수 있습니다.
꽃잎의 너비가 2 이상이면 virginica라고 강하게 확신하고
1보다 작다면 아니라고 강하게 확신하는 것을 볼 수 있습니다.
log_reg.predict([[1.5], [1.7]])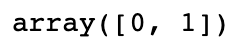
이렇게 1.5이면 0으로 virginica가 아니라고 분류하고
1.7이면 1로 virginica로 분류합니다.
이제 왜 이렇게 분류되는지 자세히 알아볼게요.
확인하기
iris1 = pd.DataFrame(iris['target'], columns=['target_names'])
iris2 = pd.DataFrame(iris['data'], columns=['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth'])
iris = pd.concat([iris1, iris2], axis=1)array로 되어있어서 불편한 점이 있어 데이터 프레임 형식으로 바꿨습니다.
target이 꽃의 종류여서 보기 편하게 pd.concat을 활용하여
하나의 데이터 프레임으로 합쳤습니다.
꽃의 너비에 해당하는 칼럼이 PetalWidth입니다.
iris.head()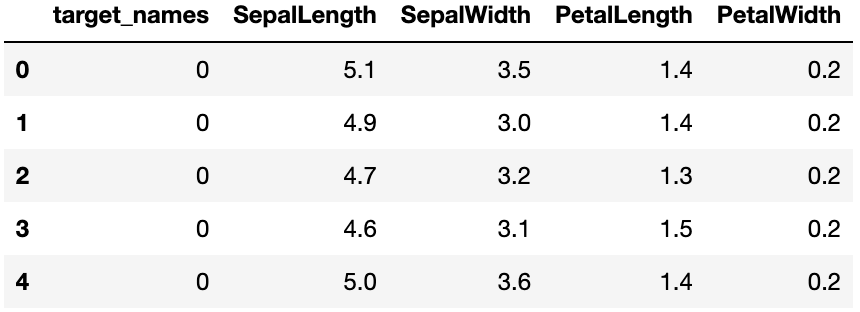
이렇게 하나의 데이터프레임으로 합쳐진 것을 확인할 수 있습니다.
iris['PetalWidth'].describe()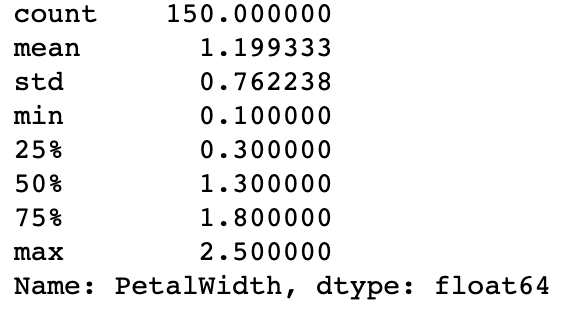
이렇게 꽃의 너비의 요약 통계량을 살펴보면
0.1 ~ 2.5까지의 분포를 나타냅니다.
그래서 아까 0~3까지의 1000개의 데이터로 돌린 것입니다.
이제 Setona, Versicolor, Virginica 각각에 대해 살펴볼게요.
Setona
iris3 = iris[(iris['target_names'] == 0)]
iris3['PetalWidth'].describe()
iris3['PetalWidth'].hist(bins=5, figsize=(10, 5))
plt.show()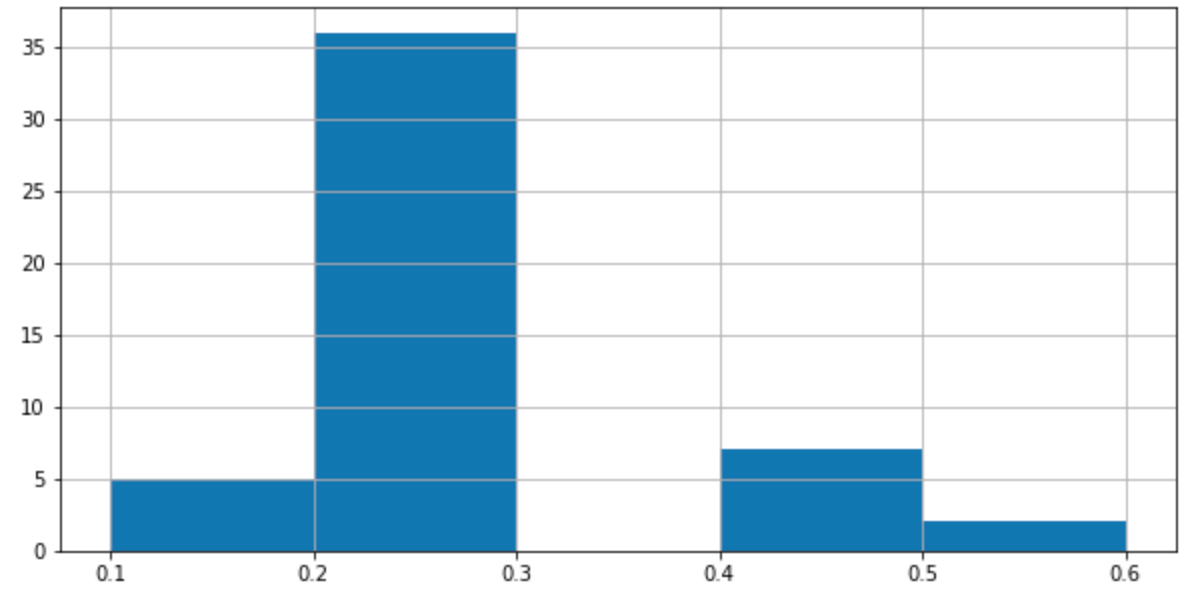
target_names가 0인 꽃의 종류가 setona인 데이터만을 뽑아서
iris3에 할당했습니다.
꽃의 너비에 관한 요약 통계량을 살펴보니
0.1 ~ 0.6까지의 분포를 나타냅니다.
따라서 위의 virginica인지 아닌지 꽃의 너비로 분류할 때
setona는 영향이 없을 것으로 추측됩니다.
Versicolor
iris4 = iris[(iris['target_names'] == 1)]
iris4['PetalWidth'].describe()
iris4['PetalWidth'].hist(bins=5, figsize=(10, 5))
plt.show()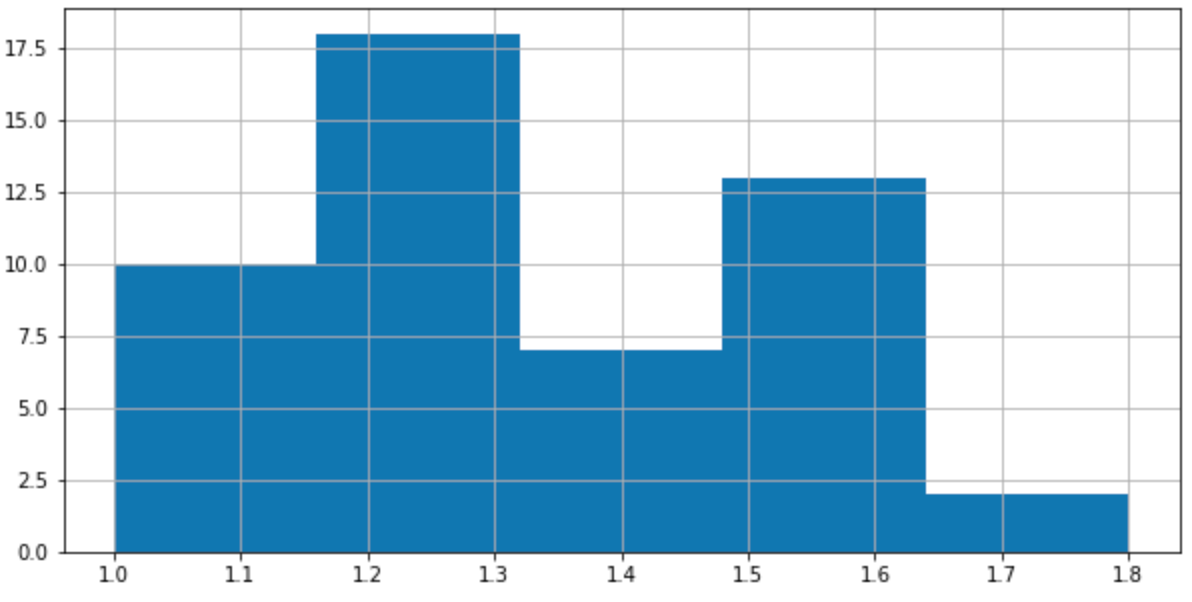
이번에는 versicolor입니다.
target_names가 1인 꽃의 종류가 versicolor인 데이터만을 뽑아서
iris4에 할당했습니다.
꽃의 너비에 관한 요약통계량을 살펴보니
1 ~ 1.8까지의 분포를 나타냅니다.
따라서 위의 virginica인지 아닌지 꽃의 너비로 분류할 때
1.6 정도에서 결정 경계가 형성된 것이
versicolor와 겹치는 부분 때문인 것으로
유추할 수 있습니다.
Virginica
iris5 = iris[(iris['target_names'] == 2)]
iris5['PetalWidth'].describe()
iris5['PetalWidth'].hist(bins=5, figsize=(10, 5))
plt.show()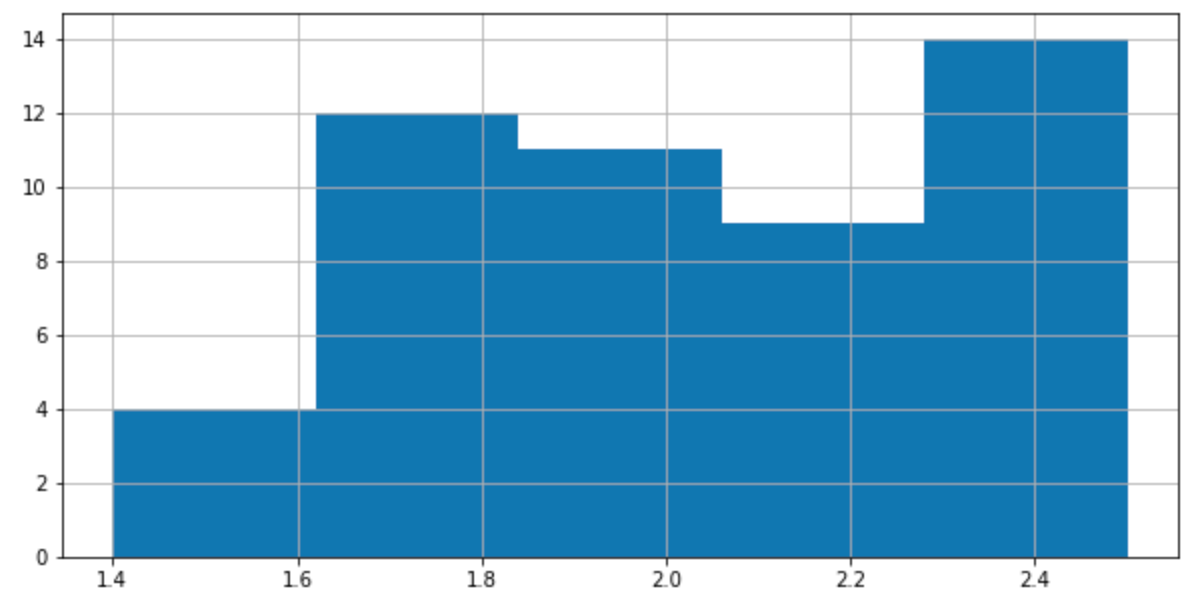
1.4 ~ 2.5 사이로 꽃의 너비가 분포합니다.
위의 versicolor가 1 ~ 1.8이므로 겹치는 것이 맞네요.
따라서 1.5는 virginica가 아니라고 분류했지만
versicolor로 분류했다고 추측할 수 있습니다.
그렇다면 마지막으로 setona인지 아닌지를 분류하여
위의 추측이 사실인지 확인해볼게요.
X = iris['data'][:, 3:] # 꽃잎의 너비
y = (iris['target'] == 0).astype(np.int) # setona면 1, 아니면 0
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X, y)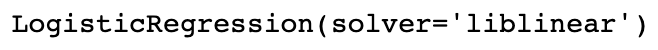
X_new = np.linspace(0, 3, 1000).reshape(-1, 1) # 0~3 사이 1000개
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], 'g-', label='Setona')
plt.plot(X_new, y_proba[:, 0], 'b--', label='Setona 아님')
plt.show()
log_reg.predict([[0.5], [0.7]])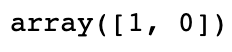
역시 결정 경계가 0.6 정도에 잡히는 것을 볼 수 있습니다.
나머지 두 종류의 꽃에 비해 꽃의 너비가 매우 작으므로
0.6 이하면 setona라고 강하게 분류하는 것을 확인할 수 있습니다!
https://www.hanbit.co.kr/store/books/look.php?p_code=B9267655530
핸즈온 머신러닝
최근의 눈부신 혁신들로 딥러닝은 머신러닝 분야 전체를 뒤흔들고 있습니다. 이제 이 기술을 거의 모르는 프로그래머도 데이터로부터 학습하는 프로그램을 어렵지 않게 작성할 수 있습니다. 이
www.hanbit.co.kr
'학회 세션 > 파인드 알파' 카테고리의 다른 글
| [Find-A] 인공 신경망 (0) | 2022.09.12 |
|---|---|
| [Find-A][Scikit Learn] 앙상블 학습 (0) | 2022.08.28 |
| [Find-A][Scikit Learn] Decision Tree (0) | 2022.08.24 |
| [Find-A] [Scikit Learn] 소프트맥스 회귀 (0) | 2022.08.20 |
| [Find-A] 파인드 알파 머신러닝이란? (1) | 2022.08.12 |



