| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 파이썬
- ML
- pandas
- 코딩테스트
- IRIS
- SQLD
- 데이터 분석
- 데이터분석
- SQL
- 머신러닝
- 데이터분석준전문가
- matplotlib
- tableau
- 시각화
- Python
- 이코테
- sklearn
- Google ML Bootcamp
- 태블로
- 이것이 코딩테스트다
- Deep Learning Specialization
- pytorch
- 딥러닝
- 회귀분석
- 자격증
- r
- scikit learn
- 데이터 전처리
- 통계
- ADsP
- Today
- Total
목록통계학과 수업 기록 (19)
함께하는 데이터 분석
 [회귀분석] 선형회귀분석 개요②
[회귀분석] 선형회귀분석 개요②
오늘은 이어서 회귀분석 때 사용할 가설검정 과정, CLT, CI에 대해 알아보겠습니다. 위의 식에서 모수 B1의 값을 구했을 때 제대로 구했는지 가설검정을 해야 합니다. 귀무가설을 베타1 = 0 대립 가설을 베타1 =/ 0이라고 놓습니다. 만약 베타1이 0이면 엄마의 키 변수가 딸의 키에 영향을 미치지 않으므로 위의 회귀식은 의미가 없어지게 되니까요. 그렇다면 가설검정의 단계를 알아볼까요? 첫 번째로 귀무가설과 대립가설을 설정하고 두 번째로 유의수준 알파를 정합니다. 이후에 분포를 찾고 p-value값을 계산합니다. 마지막으로 p-value값과 알파 값을 비교하여 p-value값이 알파 값보다 작다면 귀무가설을 기각하고 크다면 귀무가설을 기각하지 못합니다. 여기서 중요한 것은 귀무가설을 채택한다고 표현하..
 [회귀분석] 선형회귀분석 개요①
[회귀분석] 선형회귀분석 개요①
안녕하세요! 오늘은 회귀분석을 본격적으로 배우기 전 필요한 기본지식과 대략적인 소개를 하는 시간입니다. 제가 공부할 회귀분석 모델은 선형회귀분석(linear regression model)입니다. 독립변수 여러개와 종속변수 1개인 모델입니다. 종속변수가 범주형인 0과 1로 나옴에 따라 로지스틱회귀분석(logistic regression model) 이라는 것도 있지만 여기서는 다루지 않습니다. 다음학기에 범주형 자료 분석 때 기회가 된다면 살펴볼 예정입니다! 그리고 우리는 average outcome을 기반으로 할 것입니다. 평균이 아닌 중위수를 기반으로 하는 quantile regression도 있지만 여기서는 다루지 않습니다ㅠㅠ 그럼 본격적으로 시작해볼까요? 회귀분석에서 중요한 관점은 2가지 Asso..
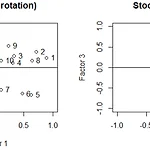 [EDA] FA with R
[EDA] FA with R
안녕하세요! 오늘은 Factor Analysis의 약자인 FA에 대해 알아보겠습니다. 파일은 저번이랑 똑같은 이 파일입니다. 만약 파일 정보가 필요하시다면 2022.02.06 - [분류 전체보기] - [EDA] PCA with R [EDA] PCA with R 오늘은 Principal Component Analysis 일명 PCA에 대해 간단한 예제를 R을 통해 알아보는 시간을 갖겠습니다! 그러기에 앞서 필요한 파일을 첨부하겠습니다. 위 데이터는 주식에 관한 10개 회사의 값입니 tnqkrdmssjan.tistory.com 여기서 확인해주세요! 그럼 시작하겠습니다. ### perfrom factor analysis with 3 factors but without any rotation kval>> Loa..
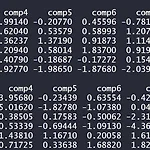 [EDA] PCA with R
[EDA] PCA with R
오늘은 Principal Component Analysis 일명 PCA에 대해 간단한 예제를 R을 통해 알아보는 시간을 갖겠습니다! 그러기에 앞서 필요한 파일을 첨부하겠습니다. 위 데이터는 주식에 관한 10개 회사의 값입니다. 그럼 시작해볼까요? rm(list=ls()) #할당변수 모두 제거 load("stockreturns.RData") #데이터 불러오기 ls() #변수 확인 >>> [1] "stocks" head(stocks) tail(stocks) str(stocks) #구조 파악 >>> 'data.frame':100 obs. of 10 variables: $ comp1 : num 0.44781 0.98811 0.87456 0.7144 0.00535 ... $ comp2 : num 0.0673 1...
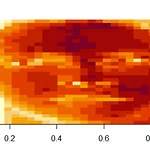 [EDA] SVD with R
[EDA] SVD with R
안녕하세요! 오늘은 Singular Value Decomposition의 약자인 SVD에 대해 R을 통해 알아보겠습니다. 우선 코딩에 필요한 파일을 올려놨습니다. 그럼 시작해볼게요! load("face.rda") #파일 불러오기 image(t(faceData)[, nrow(faceData):1]) svd1$d #singular value >>> [1] 1.977887e+01 1.513802e+01 1.213935e+01 8.427234e+00 6.200006e+00 [6] 4.936858e+00 4.402278e+00 3.967227e+00 3.743197e+00 3.017167e+00 [11] 2.967196e+00 2.406314e+00 1.899693e+00 1.555837e+00 1.492379e..
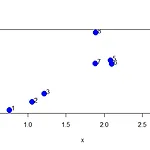 [EDA] K-Means Clustering with R
[EDA] K-Means Clustering with R
안녕하세요! 오늘은 EDA수업에서 배우는 또 다른 Clustering 기법인 k-means clustering을 R을 통해 알아보겠습니다. 간단한 좌표 설정 set.seed(1234) #rnorm으로 생성된 값 계속쓰기 위해 고정 x >> [1] 3 3 3 3 1 1 1 1 2 2 2 2 points(x, y, col = kmeansObj$cluster, pch = 19, cex = 2) image() 이용하기 par(mfrow=c(1,2)) #그래픽 1행 2열로 보이게 image(t(dataFrame)[, nrow(dataFrame):1], yaxt = "n", main = "Original Data") image(t(dataFrame)[, order(kmeansObj$cluster)], yaxt = ..
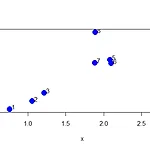 [EDA] Hierarchical Clustering with R
[EDA] Hierarchical Clustering with R
안녕하세요! 오늘은 Exploratory Data Analysis 수업에서 배우는 Clustering종류 중 Hierarchical Clustering에 대한 간단한 예제를 R코드를 통해 알아보겠습니다! 그럼 시작해볼게요! 간단한 좌표 설정 set.seed(1234) #rnorm으로 생성된 값 계속쓰기 위해 고정 x
 [수리통계학] Continuous Distributions
[수리통계학] Continuous Distributions
안녕하세요! 오늘은 Discrete Distribution의 소개에 이어서 대표적인 Continuous Distribution을 알아보겠습니다. 1. Uniform Distribution : The random variable X has a uniform distribution. 2. Exponential Distribution : In Poisson process with mean number of changes λ in the unit interval, if the random variable X denote the waiting time until the first change occurs, then distribution of X is an exponential distribution. 3. Ga..
 [수리통계학] Discrete Distributions
[수리통계학] Discrete Distributions
안녕하세요! 오늘은 대표적인 이산형 분포의 종류를 나열해보겠습니다. 1. Discrete Uniform Distribution : When a pmf is constant on the space R of X; we say that the distribution is a discrete uniform abbreviated by DU. 2. Hypergeometric Distribution : Suppose there are N1 success objects and N2 failure objects in a collection N = N1 + N2 of similar objects. When n objects are selected from these N objects at random with withou..
